Примечание.
Для доступа к этой странице требуется авторизация. Вы можете попробовать войти или изменить каталоги.
Для доступа к этой странице требуется авторизация. Вы можете попробовать изменить каталоги.
Матричные преобразования выполняют множество низкоуровневых математических вычислений трехмерной графики.
Конвейер геометрии принимает вершины в качестве входных данных. Модуль преобразования применяет мировые, видовые и проекционные преобразования к вершинам, клипирует результат и передает его в растризатор.
| Трансформация и пространство | Описание |
|---|---|
| Координаты модели в пространстве модели | В начале конвейера вершины модели объявляются относительно локальной системы координат. Это локальная отправная точка и направление. Эта ориентация координат часто называется модельное пространство. Отдельные координаты называются координатами модели. |
| Мир преобразуется в мировое пространство | Первый этап конвейера геометрии преобразует вершины модели из локальной системы координат в систему координат, которая используется всеми объектами в сцене. Процесс переориентирования вершин называется преобразованием мира, который переводит из пространственной модели в новую ориентацию, называемую мировым пространством . Каждая вершина в мировом пространстве задается с помощью в мировых координатах. |
| Преобразование представления в пространство просмотра (пространство камеры) | На следующем этапе вершины, описывающие трехмерный мир, ориентированы на камеру. То есть приложение выбирает точку зрения для сцены, а координаты мирового пространства перемещаются и поворачиваются вокруг представления камеры, превращая пространство мира в пространство просмотра (также известное как пространство камеры). Это преобразование представления, которое преобразует из мирового пространства в пространство представления. |
| Преобразование проекции в пространство проекции | Следующий этап — преобразование проекции, которое преобразует из пространства представления в пространство проекции. В этой части конвейера объекты обычно масштабируются по отношению к их расстоянию от наблюдателя, чтобы создать иллюзию глубины в сцене; близкие объекты выглядят больше, чем более удалённые объекты. Для простоты в этой документации пространство, в котором вершины существуют после преобразования проекции, обозначается как пространства проекции. Некоторые графические книги могут называть пространство проекции как постперспективное однородное пространство. Не все преобразования проекции масштабируют размер объектов в сцене. Проекция такого рода иногда называется аффинной или ортогональной проекцией. |
| Вырезка в пространстве экрана | В последней части конвейера все вершины, которые не будут видимы на экране, удаляются, чтобы растреризатор не тратил время на вычисление цветов и затенения для чего-то, что никогда не будет видно. Этот процесс называется вырезки. После вырезки остальные вершины масштабируются в соответствии с параметрами окна просмотра и преобразуются в координаты экрана. Полученные вершины, видимые на экране, когда сцена растеризована, существуют в пространстве экрана. |
Преобразования используются для преобразования геометрии объектов из одного пространства координат в другое. Direct3D использует матрицы для выполнения трехмерных преобразований. Матрицы создают трехмерные преобразования. Матрицы можно объединить для создания одной матрицы, которая охватывает несколько преобразований.
Можно преобразовать координаты между пространством модели, пространством мира и пространством просмотра.
- Мировая трансформация — преобразование из модельного пространства в мировое пространство.
- Преобразование представления — преобразование из мирового пространства в пространство вида.
- преобразование проекции — преобразуется из пространства представления в пространство проекции.
Преобразования матриц
В приложениях, работающих с трехмерной графикой, можно использовать геометрические преобразования для выполнения следующих действий:
- Выражение расположения объекта относительно другого объекта.
- Поворачивайте и изменяйте размер объектов.
- Изменение позиций, направлений и перспектив.
Вы можете преобразовать любую точку (x,y,z) в другую точку (x', y', z') с помощью матрицы 4x4, как показано в следующем уравнении.
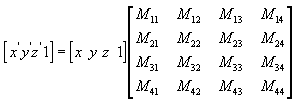
Выполните следующие уравнения (x, y, z) и матрицу, чтобы создать точку (x', y', z).
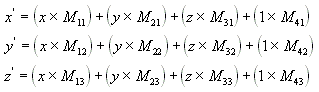
Наиболее распространенными преобразованиями являются преобразование, поворот и масштабирование. Матрицы, которые создают эти эффекты, можно объединить в одну матрицу, чтобы вычислить несколько преобразований одновременно. Например, можно создать одну матрицу для преобразования и поворота ряда точек.
Матрицы записываются в порядке столбцов строк. Матрица, которая равномерно масштабирует вершины вдоль каждой оси, известной как равномерное масштабирование, представлена в следующей матрице с помощью математической нотации.

В C++Direct3D объявляет матрицы в виде двухмерного массива с помощью структуры матрицы. В следующем примере показано, как инициализировать структуру D3DMATRIX для работы в качестве единой матрицы масштабирования (коэффициент масштабирования "s").
D3DMATRIX scale = {
5.0f, 0.0f, 0.0f, 0.0f,
0.0f, 5.0f, 0.0f, 0.0f,
0.0f, 0.0f, 5.0f, 0.0f,
0.0f, 0.0f, 0.0f, 1.0f
};
перевод
Следующее уравнение преобразует точку (x, y, z) в новую точку (x', y', z').
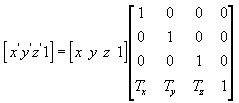
Матрицу перевода можно создать вручную в C++. В следующем примере показан исходный код функции, создающей матрицу для преобразования вершин.
D3DXMATRIX Translate(const float dx, const float dy, const float dz) {
D3DXMATRIX ret;
D3DXMatrixIdentity(&ret);
ret(3, 0) = dx;
ret(3, 1) = dy;
ret(3, 2) = dz;
return ret;
} // End of Translate
масштаб
Следующее уравнение масштабирует точку (x, y, z) произвольными значениями в направлениях x, y и z до новой точки (x', y', z').
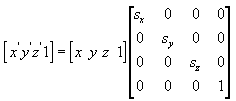
поворот
Описанные здесь преобразования предназначены для систем координат левой руки и поэтому могут отличаться от матриц преобразования, которые вы видели в другом месте.
Следующее уравнение поворачивает точку (x, y, z) вокруг оси x, создавая новую точку (x', y', z').
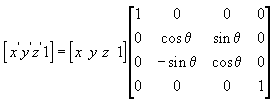
Следующее уравнение поворачивает точку вокруг оси Y.
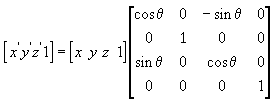
Следующее уравнение поворачивает точку вокруг оси Z.
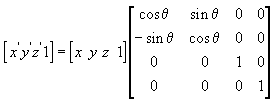
В этих примерах матриц греческая буква θ обозначает угол поворота в радианах. Углы измеряются по часовой стрелке, если смотреть вдоль оси вращения в направлении начала координат.
В следующем коде показана функция для обработки поворота по оси X.
// Inputs are a pointer to a matrix (pOut) and an angle in radians.
float sin, cos;
sincosf(angle, &sin, &cos); // Determine sin and cos of angle
pOut->_11 = 1.0f; pOut->_12 = 0.0f; pOut->_13 = 0.0f; pOut->_14 = 0.0f;
pOut->_21 = 0.0f; pOut->_22 = cos; pOut->_23 = sin; pOut->_24 = 0.0f;
pOut->_31 = 0.0f; pOut->_32 = -sin; pOut->_33 = cos; pOut->_34 = 0.0f;
pOut->_41 = 0.0f; pOut->_42 = 0.0f; pOut->_43 = 0.0f; pOut->_44 = 1.0f;
return pOut;
}
Конкатенация матриц
Одним из преимуществ использования матриц является объединение эффектов двух или нескольких матриц путем умножения их. Это означает, что для поворота модели и перевода ее в некоторое расположение не требуется применять две матрицы. Вместо этого вы умножаете матрицы поворота и перевода, чтобы создать составную матрицу, содержащую все их эффекты. Этот процесс, называемый объединением матриц, можно записать с помощью следующего уравнения.
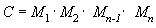
В этом уравнении C — это составная матрица, создаваемая, и M₁ до Mₙ представляют собой отдельные матрицы. В большинстве случаев сцепляются только две или три матрицы, но нет предела.
Порядок, в котором выполняется умножение матрицы, имеет решающее значение. Предыдущая формула отражает правило объединения матрицы слева направо. То есть видимые эффекты матриц, которые вы используете для создания составной матрицы, проявляются в порядке слева направо. Типичная матрица мира показана в следующем примере. Представьте, что вы создаете мировую матрицу для стереотипной летающей тарелки. Вы, вероятно, хотите вращать летающую тарелку вокруг её центра - оси Y пространства модели - и переместить её в другое место в вашей сцене. Для этого сначала создайте матрицу поворота, а затем умножьте ее на матрицу перевода, как показано в следующем уравнении.
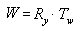
В этой формуле Ry представляет собой матрицу для поворота вокруг оси y, а Tw — преобразование в некоторое положение в координатах мира.
Порядок умножения матриц важен, так как, в отличие от умножения двух скалярных значений, умножение матрицы не является коммутативным. Умножение матриц в противоположном порядке имеет визуальный эффект перемещения летающей тарелки в её позицию в мировом пространстве, а затем вращения её вокруг начала координат мира.
Независимо от типа создаваемой матрицы помните правило слева направо, чтобы обеспечить достижение ожидаемых эффектов.
Связанные разделы