Поделиться через

Класс System.Drawing.Drawing2D.Matrix

В этой статье приводятся дополнительные замечания к справочной документации по этому API.

Класс Matrix инкапсулирует матрицу аффина 3-3, представляющую геометрическое преобразование.

В GDI+можно сохранить аффинное преобразование в объекте Matrix . Так как третий столбец матрицы, представляющий преобразование аффина, всегда равен (0, 0, 1), при создании объекта Matrix указывается только шесть чисел в первых двух столбцах. Оператор Matrix myMatrix = new Matrix(0, 1, -1, 0, 3, 4) создает матрицу, показанную на следующем рисунке.

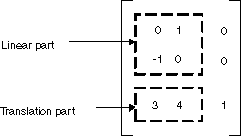
Матрица.

Замечание

В .NET 6 и более поздних версиях пакет System.Drawing.Common, который включает этот тип, поддерживается только в операционных системах Windows. Использование этого типа в кроссплатформенных приложениях вызывает предупреждения во время компиляции и исключения во время выполнения. Дополнительные сведения см. в статье System.Drawing.Common, поддерживаемой только в Windows.

Составные преобразования

Составное преобразование — это последовательность преобразований, выполняемых одно за другим. Рассмотрим матрицы и преобразования в следующем списке:

«Матрица» Преобразование
Матрица A Поворот 90 градусов
Матрица B Масштабирование по коэффициенту 2 в направлении x
Матрица C Перевод 3 единиц в направлении y

Если начать с точки (2, 1) - представленную матрицой [2 1 1] - и умножить на A, то B, то C, точка (2, 1) будет проходить три преобразования в указанном порядке.

[2 1 1]ABC = [-2 5 1]

Вместо хранения трех частей составного преобразования в трех отдельных матрицах можно умножить A, B и C вместе, чтобы получить одну матрицу 3×3, которая сохраняет все составное преобразование. Предположим ABC = D. Затем точка, умноженная на D, дает тот же результат, что и точка, умноженная на A, а затем B, а затем C.

[2 1 1]D = [-2 5 1]

На следующем рисунке показаны матрицы A, B, C и D.

Матрицы A, B, C и D

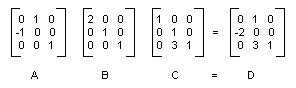
Тот факт, что матрица составного преобразования может быть сформирована путем умножения отдельных матриц преобразования означает, что любая последовательность аффинных преобразований может храниться в одном объекте Matrix.

Осторожность

Порядок составного преобразования важен. Вообще, поворот, затем масштабирование и затем перемещение — это не то же самое, что масштабирование, затем поворот и перемещение. Аналогичным образом важно, чтобы порядок умножения матрицы был важен. Как правило, ABC не совпадает с BAC.

Класс Matrix предоставляет несколько методов создания составного преобразования: Multiply, Rotate, RotateAt, Scale, Shearи Translate. В следующем примере создается матрица составного преобразования, которая сначала поворачивает 30 градусов, а затем масштабируется на коэффициент 2 в направлении y, а затем преобразует 5 единиц в направлении x:

Matrix myMatrix = new Matrix();
myMatrix.Rotate(30);
myMatrix.Scale(1, 2, MatrixOrder.Append);
myMatrix.Translate(5, 0, MatrixOrder.Append);

Dim myMatrix As New Matrix()
myMatrix.Rotate(30)
myMatrix.Scale(1, 2, MatrixOrder.Append)
myMatrix.Translate(5, 0, MatrixOrder.Append)